土木人

A點鉸接，ＢＤ點剛接，Ｃ點滾支承
各桿EI=const.
設自由度`r_1=theta_B（順時針）,r_2=theta_D（順時針）,r_3=Delta=Delta_(AB)=Delta_(BC),（均向上）
外力`{R_i}={(0),(0),(8K)]
`[K]=
`EI{(5/2,1/2,3/8),(1/2,(4sqrt(2)+3)/(4sqrt(2)),(12+3sqrt(2))/32),(3/8,(12+3sqrt(2))/32,0.3144)]

`{(r_1),(r_2),(r_3)]=[K]^(-1)*{R_i}=1/(EI)*{(-5.63),(-19),(62.8)]

不知道以上過程對不對　尤其是［Ｋ］對不對？
請多指教～謝謝～

1. 在此討論區中，若欲討論有關考題的事項，並請局限於「觀念或想法」 的討論。

2.若你對自己的觀念或想法有信心，那麼你的答案就是對的！！....考場中必須有此自信。

延續前篇文"請問靜不定剛架含剛體之勁度矩陣[K]"討論到等效力系的問題

改編自97淡江土研所結構學#四(原結構之BC桿長為8ft,CD桿長為10ft)
設自由度`r_1=theta_B(順時針), r_2=Delta=Delta_(CD)`(B點水平向右)
各桿側位移比:`Delta_(AB):Delta_(BC):Delta_(CD)`=5:3:4

由等值力系(or作功相等(咦)) `r_2=1,r_1=0,=> 50X0.75Delta=R_2XDelta`
`R_2=37.5K`
外力`{(R_1),(R_2)]={(100),(37.5)]`
請問以上計算過程不知道對不對?
謝謝~(跪拜禮new)
`[K]=EI{(0.7,-0.0525),(-0.0525,(1683/64000))]`
`{r_i}=[K]^(-1)*{R_i]=1/(EI)*{(293.8),(2012.58)]

另由傾角變位法
解得
`theta_B=293.8/(EI)
`Delta=2012.58/(EI)

1.先談一個根本性的問題，很多人都將「節點外力(joint loading)」與「等值節點外力(equivalent joint loading)」混淆了。等值節點外力，其實是節點外力的等效力系(在此也可說兩者作功相等)，也必須是相應於廣義座標之廣義力。詳細的說明，請參考「細說結構學」 p.8-14至 p.8-15。

2.在「改編自97淡江土研所結構學#四」中之圖(A)應是「節點外力」，而圖(B)才是「等值節點外力」。你可參考「細說結構學」 p.8-18 中之例3。....附帶一提，「固端內力」與「節點外力」，即圖(A)，並不是「相等」....因為在圖中用了「等號」，不知你是否有此誤解？

3.此題你用矩陣法及傾角變位法得到相同結果，那就表示兩者皆是正確的。

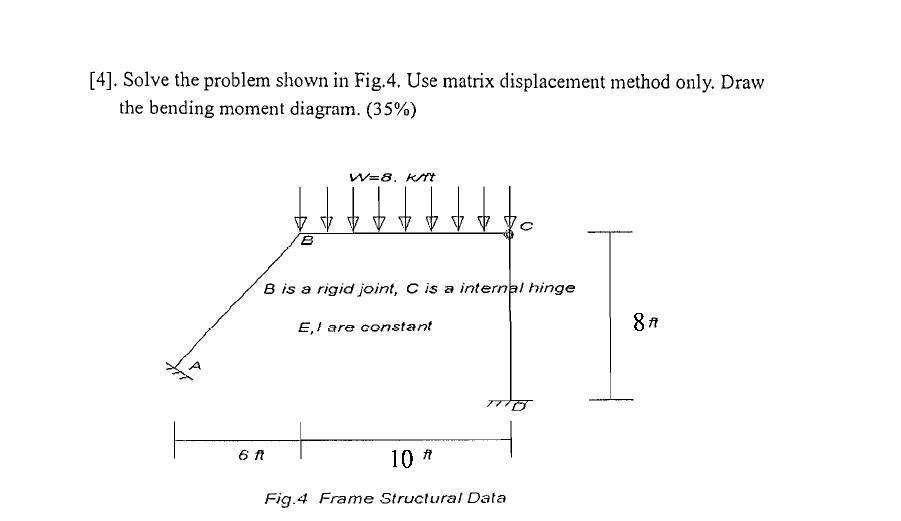
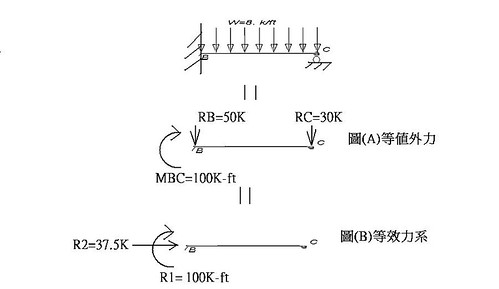
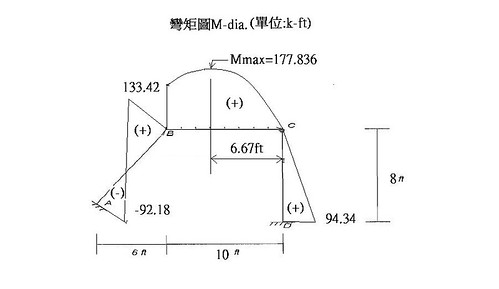
劉老師,不好意思,關於矩陣法之等值節點外力方面,再請教一個題目

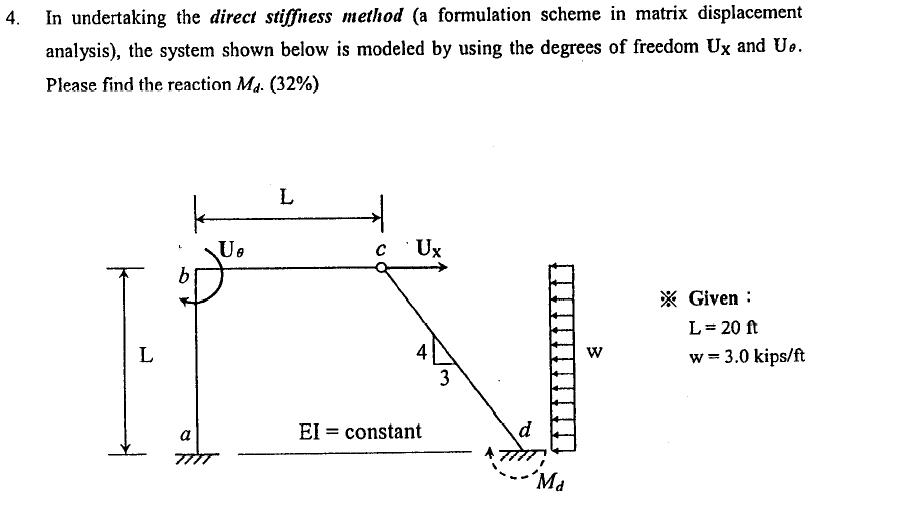
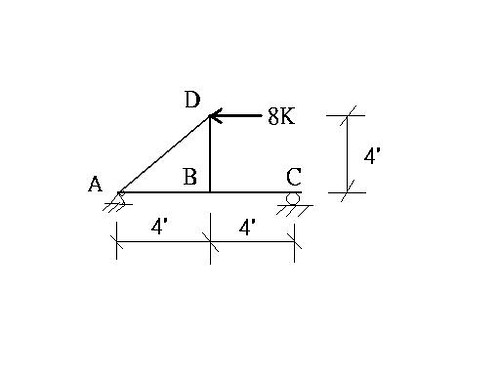
廣義座標如上圖`r_1=U_(theta),r_2=U_X=Delta`

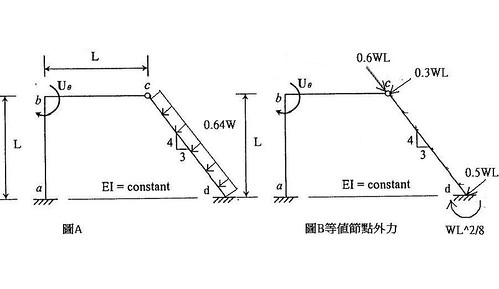
`U_X`方向上等值外力`R_2XDelta=-0.3WLX1.25Delta-0.6WLX0.6Delta`
`=>R_2=-0.735WL`(咦)
外力`{(R_1),(R_2)]={(0),(-0.735WL)]
勁度矩陣[K]=`(EI)/L{(7,-(3.75)/L),(-(3.75)/L,(1287)/(80L^2))]
`{(r_1),(r_2)]=[K]^(-1)*{R_i}=(WL)/(EI){(-(49L^2)/(1752)),(-(343L^3)/(6570))]

傾角變位法
`M_(ab)=(EI)/L(2theta_b-(6Delta)/L)
`M_(ba)=(EI)/L(4theta_b-(6Delta)/L)
`M_(bc)=(EI)/L(3theta_b+(9Delta)/(4L))
`M_(dc)=(EI)/L(-(12Delta)/(5L))+(WL^2)/8
力平衡
`sumM_b=0=>7(EI)/L*theta_b-3.75(EI)/(L^2)*Delta=0----->1
取cd桿,`sumM_c=0=>V_(dc)=(4M_(dc))/(5L)+(2WL)/5`

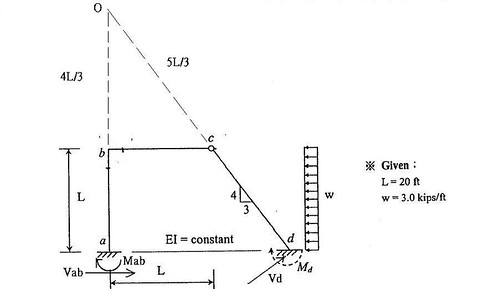
整體平衡`sumM_o=0=>M_(ab)-(M_(ab)+M_(ba))/L*(L+(4L)/3)+M_(dc)-V_(dc)*(1.25L+(5L)/3)+WL*((4L)/3+0.5L)=0`
`=>EI(-12theta_b+25.2Delta+(19WL)/(24))=0----->2
解1,2得
`theta_b=-(475WL^3)/(21024EI)
`Delta=-(665WL^4)/(15768EI)

請問從以上計算中,矩陣法與傾角變位法的答案不一樣
那麼是不是矩陣法的廣義座標`U_X`方向上`R_2=-0.735WL`計算錯誤呢?(咦)
謝謝~(跪拜禮new)

1.你可將圖中之傾斜桿件「視如」一長度為 L 之「鉛直桿」來求固端內力。
2.請參考「細說結構學」 p.8-49 例 5。