想請問有關單位力法積分
不好意思~~因為不會PO圖
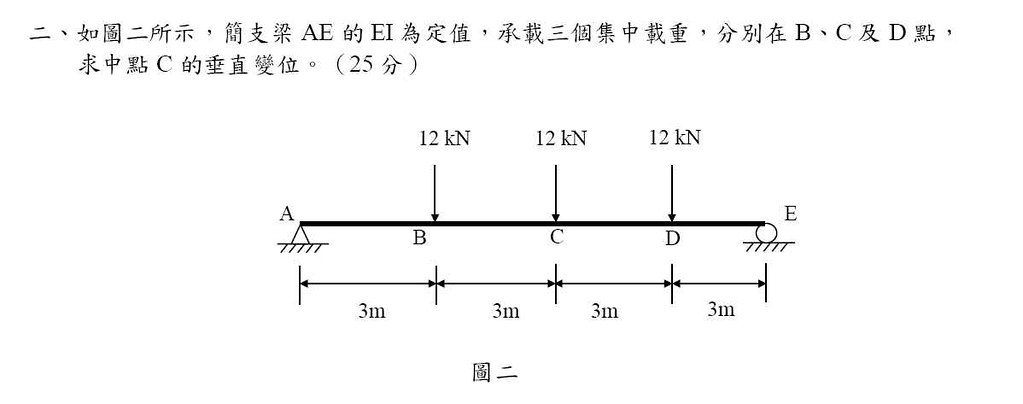
我想請問98年四等特考力學第二圖
如果用單位力積分法要怎麼積呢??
是不是
積分(0到3)(18X)(0.5X)dx+積分(0到3)(6x+54)(0.5x+0.5)dx
謝謝
我想請問98年四等特考力學第二圖
如果用單位力積分法要怎麼積呢??
是不是
積分(0到3)(18X)(0.5X)dx+積分(0到3)(6x+54)(0.5x+0.5)dx
謝謝
tgy89 寫:不好意思~~因為不會PO圖
我想請問98年四等特考力學第二圖
如果用單位力積分法要怎麼積呢??...
tgy89 寫:不好意思~~因為不會PO圖
我想請問98年四等特考力學第二圖
如果用單位力積分法要怎麼積呢??
mayerhof0920 寫:學生一點想法,提供參考~
1.先求出A,E兩點的支承反力,並以C點為固定端繪製M/EI圖
2.施加一單位力於C點,同樣以C點為固定端繪製m圖
3.由單位力法1*c點位移=(A1*Y1+A2*Y2)*2
其中A1和A2分別為支承反力和集中外力在M/EI圖的面積
如有謬誤,還望老師和板上前輩指正~
George118 寫:這題來說,小弟不會使用"單位力法之體積積分",
不過依照後學的思考思維來說,應該也可以使用"彎矩力矩法",
計算方式可以分為兩部份,
一、中間的力,可以使用重疊法的公式求出撓度。
二、計算左側的力,可以使用彎矩力矩法求出撓度,再乘上2
(因為左右兩側力對稱,所以撓度要乘上2)。
由(一)(二)計算而出的撓度互加,即可得知此題之C點總撓度。