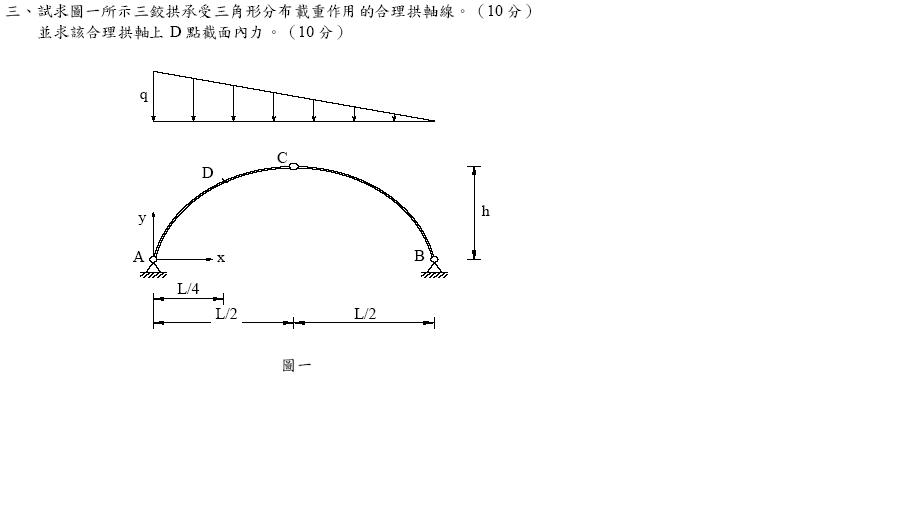
週末動動腦--好題目分享【96年建築師】結構系統第3題第2小題
題目請參考考選部網站。
幫人(?)解的,我剛解出的答案是
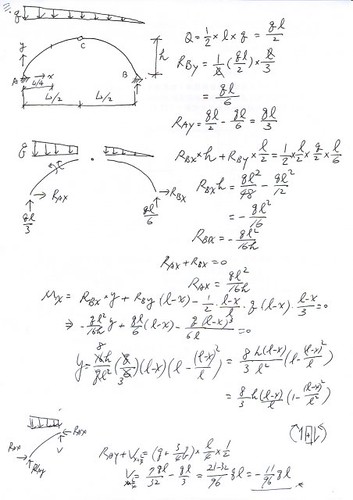
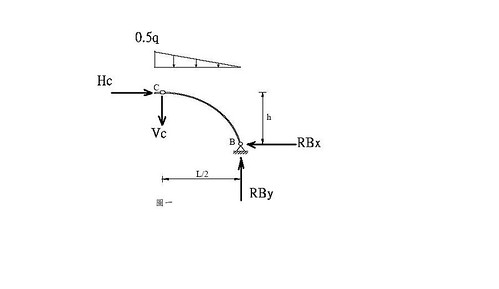
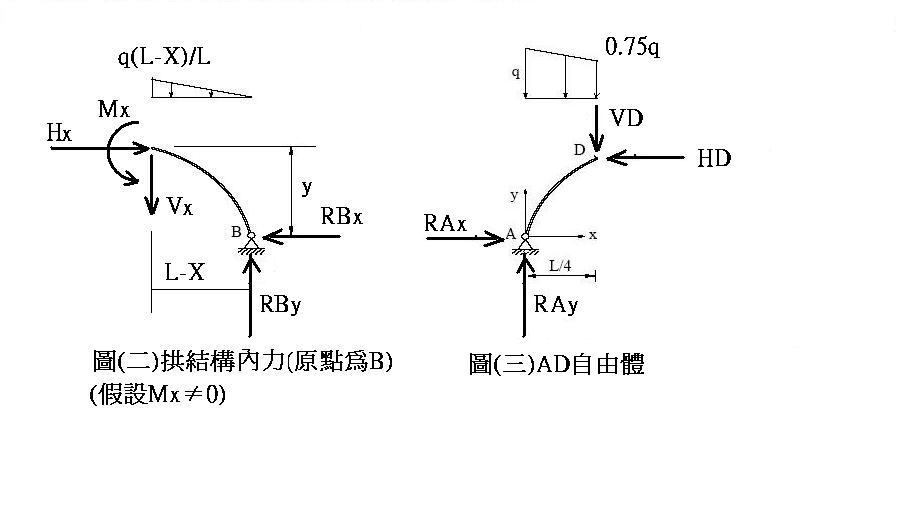
`M_D=(15/128)*q*L^2`(不見得正確)
其他的反力`A_V=2/3*q*L`(↑) `A_H=(1/(12*h))*q*L^2`(→)
三鉸拱在96年的國考中還真熱門啊!不過這配分僅給10分個人是嫌少了!
準建築師們遇到這種考題應該在考場的臉色都不好看吧!(廢話,要我只有10分我也不解)
通常國考的配分與計算時間是一致的,也就是出題教授認為這一子題只需10分鐘就可以瞬殺。
挑戰來了!這題題目大家要解多久呢?(假設使用FX-82)
(A)10分鐘 (B)15分鐘 (C)20分鐘 (D)大於21分鐘
說說您的作法吧!小弟是(B) 。
。
幫人(?)解的,我剛解出的答案是
`M_D=(15/128)*q*L^2`(不見得正確)
其他的反力`A_V=2/3*q*L`(↑) `A_H=(1/(12*h))*q*L^2`(→)
三鉸拱在96年的國考中還真熱門啊!不過這配分僅給10分個人是嫌少了!
準建築師們遇到這種考題應該在考場的臉色都不好看吧!(廢話,要我只有10分我也不解)
通常國考的配分與計算時間是一致的,也就是出題教授認為這一子題只需10分鐘就可以瞬殺。
挑戰來了!這題題目大家要解多久呢?(假設使用FX-82)
(A)10分鐘 (B)15分鐘 (C)20分鐘 (D)大於21分鐘
說說您的作法吧!小弟是(B)