土木人

請問版上各位高手：

我在歐陽「解說結構學」一書上，
上頭說卡氏第二定理，無法用於「溫差、沈陷」等問題上，
但我在其它的書上，卻有用卡氏第二定理、最小功法來求解這類請不定結構的問題
想請教說
卡氏定理，到底能不能用在「溫差、沈陷」等問題上

謝謊

kkk0912 寫:請問版上各位高手：

我在歐陽「解說結構學」一書上，
上頭說卡氏第二定理，無法用於「溫差、沈陷」等問題上，
但我在其它的書上，卻有用卡氏第二定理、最小功法來求解這類請不定結構的問題
想請教說
卡氏定理，到底能不能用在「溫差、沈陷」等問題上

謝謊

卡二是應變能對「外力」一次偏微分求變位
溫差不是一個固定的外力，所以單純卡二CASE無法求溫差造成的變位。
這是第一個理由！

第二個重要的理由是
靜定結構受溫差，會自己調整結構形狀，所以不會有內力產生。根本不用求。

你說的應用我想應該不是在單純卡二（靜定）的CASE，應該是最小功法（靜不定）的應用吧！

溫差靜不定的結構確實可以用最小功法來解內力。

至於變位也是可以解的，例如利用虛補功法的延伸，可以算柔度矩陣，矩陣一出，通通可以求。

紫煌大
請問一下 卡二不能用在非線性的理由
除了應力應變圖上應變能及補應變能面積不相等作為說明之外
計算上的意義是因為各桿內力與材料性質無關,所以積分時要對力量或應力`sigma`積分嗎?
舉例來說:

上圖中材料性質`sigma=sqrt(epsilon)`,斷面積A
D端贅力S
補應變能U*=`intepsilondsigma=intsigma^2dsigma=(sigma^3)/3`
AB桿U*=`(((2P-S)/A)^3)/3`
對S偏微`(delU^(star))/(delS)=-((2P-S)^2)/(A^3)`

應變能U=`intsigmadepsilon=intsqrt(epsilon)depsilon=(2epsilon^(3/2))/3=(2sigma^3)/3`
AB桿U=`(2((2P-S)/A)^3)/3`
對S偏微`(delU)/(delS)=-(2(2P-S)^2)/(A^3)`
很明顯的`U^(star)!=U`
其中原因是因為各桿內力與材料性質無關,所以積分時要對應力`sigma`積分?(咦)
不知道這樣觀念對嗎?(我在很多書上找不到比較可以理解的說法...)
例如歐陽的[材料力學論衡]P14-28頁說:為何要求結構需彈性呢?
因為導證過程中我們仰賴應變能U這個單值函數(咦),非彈性結構不存在單值函數,
問題是什麼是單值函數呢?跟我講的各桿內力與材料性質無關是類似的意思嗎?
請紫煌大幫忙一下
謝謝~(跪拜禮new)

laimaddux31 寫:紫煌大
請問一下 卡二不能用在非線性的理由
除了應力應變圖上應變能及補應變能面積不相等作為說明之外
計算上的意義是因為各桿內力與材料性質無關,所以積分時要對力量或應力`sigma`積分嗎?
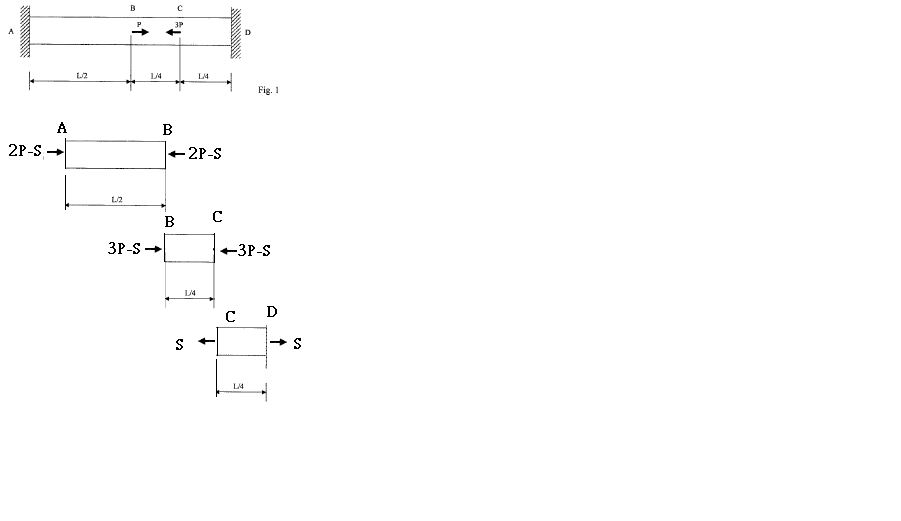
舉例來說:
很明顯的`U^(star)!=U`
其中原因是因為各桿內力與材料性質無關,所以積分時要對應力`sigma`積分?(咦)
不知道這樣觀念對嗎?(我在很多書上找不到比較可以理解的說法...)
例如歐陽的[材料力學論衡]P14-28頁說:為何要求結構需彈性呢?
因為導證過程中我們仰賴應變能U這個單值函數(咦),非彈性結構不存在單值函數,
問題是什麼是單值函數呢?跟我講的各桿內力與材料性質無關是類似的意思嗎?
請紫煌大幫忙一下
謝謝~(跪拜禮new)

ㄟ..力學有三個分析步驟
變形諧和，材料性質，平衡條件

假設一個簡支剛性桿件中點受集中力P，那麼兩端的反力永遠是`P/2`

即使其中一端變成彈簧，另一端變成阻尼，反力一樣是`P/2`

您說的「各桿內力與材料性質無關」即為此意！（剛性桿並不會儲存應變能！）

因為只用到平衡條件這個觀念！

用同一個例子！若簡支剛梁的兩點都是支承，那應變能好解，也是你說的單值函數。

若一邊是阻尼，一邊是彈簧，因為黏彈性的關係，應變能變成不好解，也是你說的非單值函數。

若加上桿件本身非剛性，則這個系統就更複雜了！

如您舉的例子，若中段是黏彈性的材料，很肯定的，各桿內力必與材料性質有關！

不過如何有關，要看施加的力量的動力型態，因為黏彈性材料會吸收能量（產生遲滯迴圈）！

這方面請參考黏力的書！

卡二的前身是「C開頭I結尾的某定理」與虛補功原理...

他的描述是「對補能取力量一次偏微分得變位」，因為線彈性，補能等於應變能，卡二才能適用

所以您說補能與應變能面積不同（其實是函數不同）故卡二僅能在線彈性使用，是對的！

這也是最簡單的解釋！