98年高員三級結構學第一題求解…
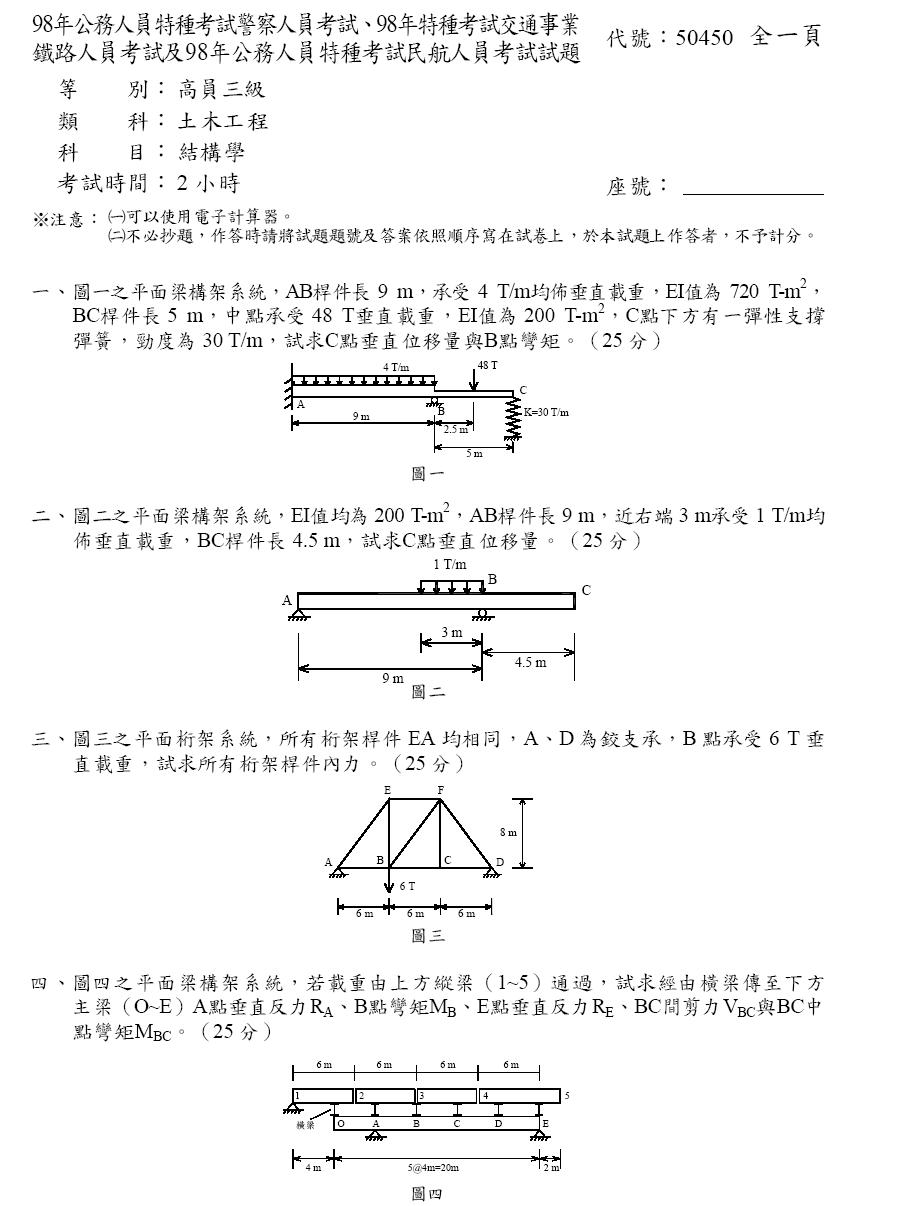
第一題不曉得能不能請紫煌大大用彎矩分配法解解看~~~
ps:小弟已經用直接勁度法求解了,雖然對了,但總覺得要算3x3的逆矩陣很容易出錯,所以看是不是能用綜合彎矩分配法求解…

sharefile92 寫:
第一題不曉得能不能請紫煌大大用彎矩分配法解解看~~~
ps:小弟已經用直接勁度法求解了,雖然對了,但總覺得要算3x3的逆矩陣很容易出錯,所以看是不是能用綜合彎矩分配法求解…
b516 寫:該題只有一個彎矩分配節點,不需用到綜合彎矩分配法求解吧
sharefile92 寫:b516 寫:該題只有一個彎矩分配節點,不需用到綜合彎矩分配法求解吧
嗯?就是用頂住+鬆開方式去求解嗎?
因為彈簧c點有一變位,想說是不是能像綜合彎矩分配法方式來算算看…
就不用再頂住、鬆開的方式去求解了,但我用綜合彎矩分配法解出來的答案卻不對…
b516 寫:sharefile92 寫:b516 寫:該題只有一個彎矩分配節點,不需用到綜合彎矩分配法求解吧
嗯?就是用頂住+鬆開方式去求解嗎?
因為彈簧c點有一變位,想說是不是能像綜合彎矩分配法方式來算算看…
就不用再頂住、鬆開的方式去求解了,但我用綜合彎矩分配法解出來的答案卻不對…
我用彎矩分配法算題目到現在,從來就沒用啥頂住+鬆開方式去求解,直接把桿端彎矩(外力加側移)列出,然後列表計算,最後用力平衡求未知數X,如此而已,縱合彎矩分配法是適用二個以上彎矩分配節點,歐陽結構學書上都寫的很清楚
不是看歐陽的書@@…所以這種題目就不能用綜合彎矩分配法嘍?殘念.....


chemicalgirl 寫:這題我用綜合彎矩分配法算
Mab = -16.29
Mba = 48.42
Mbc = -48.42 tf-m
C點垂直變位 0.4772 m (↓)
請問我有算對嗎?
sharefile92 寫:chemicalgirl 寫:這題我用綜合彎矩分配法算
Mab = -16.29
Mba = 48.42
Mbc = -48.42 tf-m
C點垂直變位 0.4772 m (↓)
請問我有算對嗎?
對耶~~~不曉得怎麼算的,可以分享一下嗎?
我之前也有算過彈簧的,有的可以解出來,但這一題解出來的答案就跟正確答案不一樣。
ps:太久沒上來看了,「1003」大大的文章沒有看到@@,圖片也失效了。