贊助商廣告
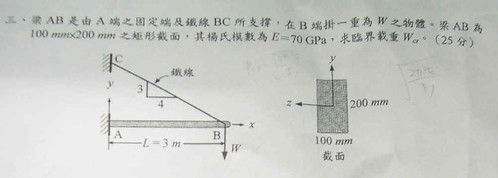
上面的圖是借版友chengyu66的
該題大家討論出來的答案不一,
關鍵都在鐵線條件未給,不知如何下手......
請問老師您認為k應該取多少才對?
B點究竟要當成定向支承, 自由端, 鉸支承, 或是要另外再堆導一個?
懇請您幫忙解惑,感激不盡
現在的時間是 2026 2月 08 (週日) 5:58 pm
版主: 老師


Domon 寫:
上面的圖是借版友chengyu66的
該題大家討論出來的答案不一,
關鍵都在鐵線條件未給,不知如何下手......
請問老師您認為k應該取多少才對?
B點究竟要當成定向支承, 自由端, 鉸支承, 或是要另外再堆導一個?
懇請您幫忙解惑,感激不盡

Domon 寫:上面的圖是借版友chengyu66的
該題大家討論出來的答案不一,
關鍵都在鐵線條件未給,不知如何下手......

trlct 寫:Domon 寫:上面的圖是借版友chengyu66的
該題大家討論出來的答案不一,
關鍵都在鐵線條件未給,不知如何下手......
A:
1.當挫屈發生在xy平面時,A端固定,B端如同鉸支承,K=0.7。(使用Iz)
2.當挫屈發生在xz平面時,A端固定,B端如同自由端,K=2。(使用Iy)
3.比較兩種狀況,取較小之Pcr值。


laimaddux31 寫:在題目所示圖上是XY平面
繩索束制B端 Y向
在XZ平面上 看起來就是懸臂樑
繩索並沒有作用
你可以想像XZ平面是桌面,繩索放在桌面上一端固定一端滾支
繩索垂直桌面向被你提起時因為忽略小變形
所以繩索沒有受張力
一般合理假設是樑的EI=const,,EA->`oo`也就是忽略軸向變形
繩索只考慮EA=const.,而沒有EI
所以假設B端垂直向位移`Delta`
繩索`(EA)/(1.25L)`=`K_s`
B端垂向力w'=`w_(cr)-0.36K_s*Delta`
B點軸向壓力N=`0.48K_S*Delta`
A點為原點,X處力矩M(X)=`w'(L-X)+N(L-Delta)`
EIy(X)=M(X)
設`beta^2=N/(EI)`
最後解得特徵方程式`tan(beta*L)=(N*beta(Delta-(W')/N))/(w')`
但是繩索勁度`K_s`未知情況下
上述特徵方程式沒辦法解挫屈載眾`W_(cr)`
所以假設`Delta=0`去求解是OK的
`
laimaddux31 寫:細長比KL/r
y軸:
`K_y`=2,迴轉半徑`r_y=sqrt((I_y)/A)=sqrt((200*100^3/12)/(200*100))=28.868`
Z軸:
`K_Z`=0.7,迴轉半徑`r_z=sqrt((I_z)/A)=sqrt((100*200^3/12)/(200*100))=57.735`
細長比`(k_Z*L)/(r_Z)<(K_y*L)/(r_y)`
`:.`y軸挫屈
挫屈載重`W_(cr)=1.439MN`

laimaddux31 寫:假設鐵線剛度為EA
則鐵線受拉力T=`(20W)/((125I_z)/(AL^2)-12)`
然後你可以推導挫屈特徵方程式(如前述)
但是鐵線斷面積A未知,沒法求解出`W_(cr)`
